In machine learning, the performance of a model heavily depends on its parameters, hyperparameters, and the data used for training. Fine-tuning these parameters can drastically improve model accuracy and efficiency, but it requires a deep understanding of optimization techniques and validation methods. This article explores three primary optimization techniques: Grid Search, Random Search[1], and Bayesian Optimization[2], comparing their strengths, weaknesses, and applications, especially in complex models.
We’ll delve into the theoretical foundations, practical considerations, coding examples, and also cover essential aspects of model evaluation, focusing on hyperparameters, cross-validation techniques, and performance assessment.
1. Understanding Hyperparameters and Their Role in Model Optimization
In machine learning, hyperparameters are parameters set before training begins and remain constant during model training. Unlike parameters learned directly from the data, hyperparameters dictate how the training process unfolds. Selecting the right hyperparameters can be challenging, especially in complex models with numerous hyperparameters.
Common examples of hyperparameters include:
Learning rate: Determines the step size for updating weights.
Batch size: The number of training samples used in one forward/backward pass.
Number of layers: In deep learning models, this specifies the depth of the model.
Regularization parameter: Prevents overfitting by penalizing large weights.
Adjusting these values is crucial as they significantly impact model convergence, speed, and accuracy. This optimization process is often called hyperparameter tuning.
2. Validation Techniques in Model Optimization
Before diving into optimization methods, understanding validation techniques is essential. Validation helps evaluate a model's performance on unseen data, ensuring it generalizes well rather than just fitting the training data.
The most commonly used validation technique is cross-validation, where the data is split into multiple subsets:
K-Fold Cross-Validation: The dataset is divided into k subsets or "folds." Each fold is used as a validation set while the remaining folds train the model. This is repeated k times to provide a robust performance metric.
Leave-One-Out Cross-Validation (LOOCV): A special case of k-fold cross-validation where k equals the number of samples, leaving out only one sample as validation for each training iteration.
Cross-validation helps determine whether a hyperparameter setting improves generalization, which is the ultimate goal of model optimization.
3. Hyperparameter Optimization Techniques
Several optimization methods can find the best combination of hyperparameters. The most widely used techniques are Grid Search, Random Search, and Bayesian Optimization.
3.1 Grid Search
Overview
Grid Search is a brute-force method for hyperparameter tuning, systematically exploring all combinations within a specified range of hyperparameters. For each hyperparameter combination, Grid Search trains and evaluates the model on the validation set, identifying the combination that yields the best performance.
Grid Search is straightforward to implement and guarantees finding the optimal solution within the search space.
Pros and Cons
Pros: Comprehensive, simple, guarantees finding the best solution if all possible combinations are tried.
Cons: Computationally expensive, especially with large datasets or complex models. Inefficient for models with many hyperparameters.
Code Example
Here’s an example of implementing Grid Search for hyperparameter tuning using scikit-learn on a Support Vector Machine [5] using the Iris Dataset[4]:
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# Load dataset and split
data = load_iris()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2, random_state=42)
# Define the parameter grid
param_grid = {
'C': [0.1, 1, 10, 100],
'gamma': [1, 0.1, 0.01, 0.001],
'kernel': ['rbf', 'linear']
}
# Initialize and fit GridSearchCV
grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=2, cv=5)
grid.fit(X_train, y_train)
# Print best parameters
print("Best Hyperparameters:", grid.best_params_)
print("Best Score:", grid.best_score_)3.2 Random Search
Overview
Random Search selects random combinations of hyperparameters, as opposed to Grid Search, which exhaustively evaluates each combination. This approach is often more efficient in high-dimensional spaces, where Grid Search’s exhaustive approach becomes infeasible.
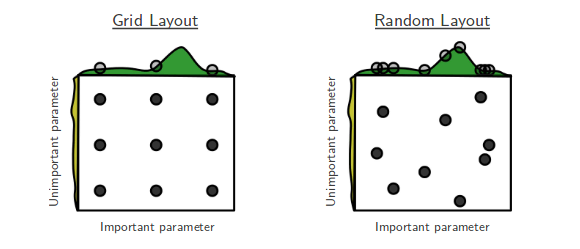
Pros and Cons
Pros: Efficient in high-dimensional spaces, provides reasonable performance with fewer evaluations.
Cons: No guarantee of finding the optimal solution; performance depends on the range of randomly selected hyperparameters.
Code Example
Implementing Random Search is similar to Grid Search but uses
RandomizedSearchCV instead of GridSearchCV
from sklearn.model_selection import RandomizedSearchCV
from sklearn.ensemble import RandomForestClassifier
from scipy.stats import randint
# Load dataset and split
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2, random_state=42)
# Define the parameter distribution
param_dist = {
'n_estimators': randint(50, 200),
'max_depth': randint(1, 10),
'min_samples_split': randint(2, 11),
'min_samples_leaf': randint(1, 5)
}
# Initialize and fit RandomizedSearchCV
random_search = RandomizedSearchCV(RandomForestClassifier(), param_dist, n_iter=20, cv=5, random_state=42)
random_search.fit(X_train, y_train)
# Print best parameters
print("Best Hyperparameters:", random_search.best_params_)
print("Best Score:", random_search.best_score_)3.3 Bayesian Optimization
Overview
Unlike Grid and Random Search, Bayesian Optimization models the function to be optimized. It iteratively improves by balancing exploration (trying new hyperparameter values) and exploitation (fine-tuning around high-performing values). Bayesian Optimization often leverages a Gaussian Process (GP) to model the objective function, although other models like Tree-structured Parzen Estimators (TPE) can also be used.
Pros and Cons
Pros: Efficient, well-suited for complex models, usually requires fewer evaluations to reach optimal solutions.
Cons: Computationally intensive due to building a probabilistic model; implementation is more complex than Grid or Random Search.
Code Example with Hyperopt
The following example demonstrates Bayesian Optimization with the hyperopt library.
from hyperopt import fmin, tpe, hp, Trials
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifier
import numpy as np
# Define the objective function
def objective(params):
model = GradientBoostingClassifier(**params)
accuracy = cross_val_score(model, X_train, y_train, cv=5).mean()
return -accuracy # Minimize the negative accuracy for maximization
# Define the parameter space
param_space = {
'n_estimators': hp.choice('n_estimators', range(50, 200)),
'max_depth': hp.choice('max_depth', range(1, 10)),
'learning_rate': hp.uniform('learning_rate', 0.01, 0.3),
}
# Run Bayesian Optimization
trials = Trials()
best_params = fmin(fn=objective, space=param_space, algo=tpe.suggest, max_evals=50, trials=trials)
# Print best parameters
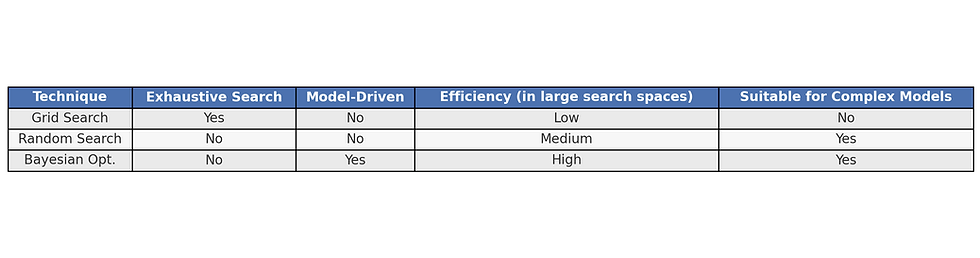
print("Best Hyperparameters:", best_params)4. Comparison of Optimization Techniques
In practice, Grid Search is preferred when the parameter space is limited, while Random Search is effective for higher-dimensional spaces. Bayesian Optimization is generally best for complex models where evaluations are expensive, as it requires fewer trials to find optimal solutions.
5. Evaluating Model Performance
After optimizing a model’s hyperparameters, evaluating its performance is crucial to ensure it generalizes well to new data. Model performance evaluation not only verifies that the chosen hyperparameters yield the best possible results on training and validation data but also checks if the model performs well on completely unseen data. This section explores various evaluation metrics, their applications, and how to interpret them effectively, as well as common visualization tools.
5.1 Evaluation Metrics
The choice of evaluation metric depends largely on the type of machine learning task, such as classification, regression, or clustering. Each type has distinct metrics suited to different performance aspects.
For Classification Tasks
Accuracy: The proportion of correctly predicted samples out of the total samples. Although widely used, accuracy can be misleading when dealing with imbalanced datasets, as it doesn’t account for false positives and false negatives.
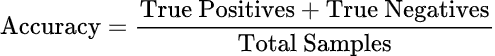
Precision: Measures the accuracy of positive predictions. Precision is particularly useful in cases where false positives are costly (e.g., fraud detection).

Recall: Indicates the model's ability to identify all relevant instances. Recall is essential when missing true positives has significant consequences (e.g., medical diagnoses).

F1-Score: The harmonic mean of precision and recall, providing a balance when both metrics are equally important.

ROC-AUC Score [3]: The Area Under the Receiver Operating Characteristic Curve (ROC-AUC) is a common metric for binary classifiers, especially when class balance is an issue. The ROC curve plots the true positive rate against the false positive rate, providing a visualization of the model's performance at various thresholds.
For Regression Tasks
Mean Absolute Error (MAE): Measures the average absolute differences between predicted and actual values. It is useful for interpreting error in the same units as the target variable.
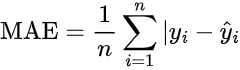
Mean Squared Error (MSE): Calculates the average of squared errors, emphasizing larger errors due to squaring. This metric is valuable when penalizing larger errors is desired.

Root Mean Squared Error (RMSE): The square root of MSE, RMSE is interpretable in the same units as the target and penalizes larger errors more heavily.
R-Squared: Represents the proportion of variance in the target variable explained by the model. A high R-squared value indicates a well-fitting model, but it is essential to consider that an overly high R-squared could also mean overfitting.
5.2 Confusion Matrix
A confusion matrix is a popular visualization tool for classification models. It displays the true positive, true negative, false positive, and false negative counts in a matrix format, providing a detailed look at where the model might be making mistakes.
For instance, in binary classification, a confusion matrix might look like this:
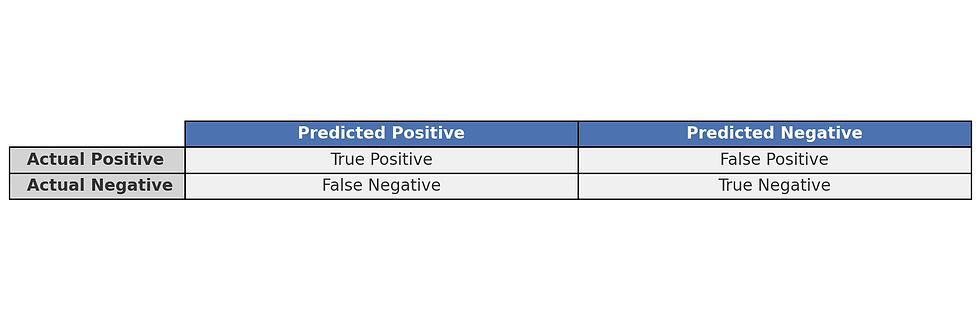
From this, precision and recall can be computed to gain further insights into the model’s performance on positive and negative classes. A well-balanced confusion matrix indicates that the model performs well across all classes, while imbalances can signal the need for further optimization.
5.3 K-Fold Cross-Validation Performance Tracking
K-Fold Cross-Validation is often used to validate model performance across multiple splits of the data. By splitting the dataset into k subsets (folds) and iteratively training the model on k-1 folds while validating the remaining fold, this technique provides a robust assessment of the model’s stability and performance.
Cross-validation helps ensure that the evaluation metric represents the model’s performance across the entire dataset, preventing the overfitting or underfitting issues that might arise from evaluating on a single train-test split. This approach is particularly useful for tuning models with small datasets.
Using scikit-learn, K-Fold Cross-Validation can be implemented as follows:
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier
# K-Fold Cross Validation
scores = cross_val_score(RandomForestClassifier(), X, y, cv=5)
print("Cross-Validation Scores:", scores)
print("Mean CV Score:", scores.mean())5.4 Learning Curves
Learning curves plot the model’s performance (often accuracy or loss) against the training epochs or size of the training dataset. They provide insight into the model’s behavior during training and can help diagnose underfitting or overfitting.
Underfitting: When both training and validation accuracy are low, the model may be underfitting, indicating that it is too simple to capture the patterns in the data. This may require either increasing the model’s complexity or further tuning hyperparameters.
Overfitting: If training accuracy is high while validation accuracy is low, the model may be overfitting, meaning it’s memorizing the training data rather than generalizing. Regularization techniques, cross-validation, or more data might help reduce overfitting.
Convergence: A model that has converged will show both training and validation performance leveling out as epochs progress. This indicates that further training will likely not improve performance and signals a good stopping point.
Learning curves can be generated using libraries such as matplotlib or scikit-learn and are beneficial for tracking model performance across time, particularly for deep learning models that require many epochs of training.
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
import numpy as np
# Example: Plotting a learning curve for a RandomForestClassifier
train_sizes, train_scores, valid_scores = learning_curve(
RandomForestClassifier(), X_train, y_train, cv=5, n_jobs=-1,
train_sizes=np.linspace(0.1, 1.0, 5)
)
plt.plot(train_sizes, np.mean(train_scores, axis=1), label='Training Score')
plt.plot(train_sizes, np.mean(valid_scores, axis=1), label='Validation Score')
plt.xlabel('Training Set Size')
plt.ylabel('Score')
plt.title('Learning Curve')
plt.legend()
plt.show()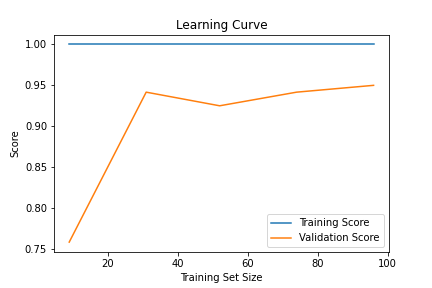
5.5 Finalizing Model Selection
Ultimately, the decision of which model and optimization technique to deploy depends on a combination of performance metrics, interpretability, computational efficiency, and scalability. This can be formalized into a model selection pipeline, ensuring that the model chosen is optimal not only in terms of predictive performance but also across practical constraints.
A comprehensive model selection workflow might look like this:
Define Model Goals: Outline whether accuracy, interpretability, efficiency, or scalability is the highest priority.
Perform Hyperparameter Tuning: Use Grid Search, Random Search, or Bayesian Optimization to explore potential hyperparameters.
Cross-Validation and Performance Tracking: Validate the models through cross-validation, recording all metrics.
Visualization of Results: Use visualization tools to assess the best-performing models across multiple criteria.
Model Evaluation on Test Data: Assess the chosen model on unseen test data to confirm generalization.
Deployment Considerations: Ensure that the final model is deployable and meets all practical requirements.
By carefully following these steps and applying a balanced approach to hyperparameter optimization and validation, practitioners can ensure that their models are both robust and practical for real-world applications. This careful balance is the hallmark of successful machine learning model deployment and is essential for delivering value from machine learning projects.
6. Conclusion
Hyperparameter tuning is a crucial step for building effective machine learning models. This article explored Grid Search, Random Search, and Bayesian Optimization, emphasizing their use cases, advantages, and limitations. By leveraging these techniques, practitioners can enhance model performance, reduce overfitting, improve generalization, and optimize key evaluation metrics such as accuracy, precision, recall, F1 Score, and ROC-AUC.
For complex, high-dimensional models, Bayesian Optimization is typically the most efficient. However, for smaller models, Random Search or even Grid Search may suffice. Each method has its place, and understanding these techniques and their impact on evaluation metrics allows data scientists and ML engineers to fine-tune models efficiently, ensuring robust, high-performing models for real-world applications.
References
[1] Bergstra, J., & Bengio, Y. (2012). Random search for hyper-parameter optimization. Journal of machine learning research, 13(2).
[2] Snoek, J., Larochelle, H., & Adams, R. P. (2012). Practical bayesian optimization of machine learning algorithms. Advances in neural information processing systems, 25.
[3] Fawcett, T. (2006). An introduction to ROC analysis. Pattern recognition letters, 27(8), 861-874.
[4] The Iris Dataset, Sickt-Learn
[5] Cortes, C. (1995). Support-Vector Networks. Machine Learning.


Comments